Networks in cosmology
Marián Boguñá
The causal structure of spacetime and standard cosmological models can be easily mapped into hyperbolic geometry. Quite interestingly, networks that arise in this context are extremely similar to networks we find in domains as diverse as cell biology, social sciences, or socio-technological systems, like the Internet or the world wide web.
Relevant references
Emergence of Soft Communities from Geometric Preferential Attachment
Konstantin Zuev, Marián Boguñá, Ginestra Bianconi, and Dmitri Krioukov
Scientific Reports
(2015)
abstract
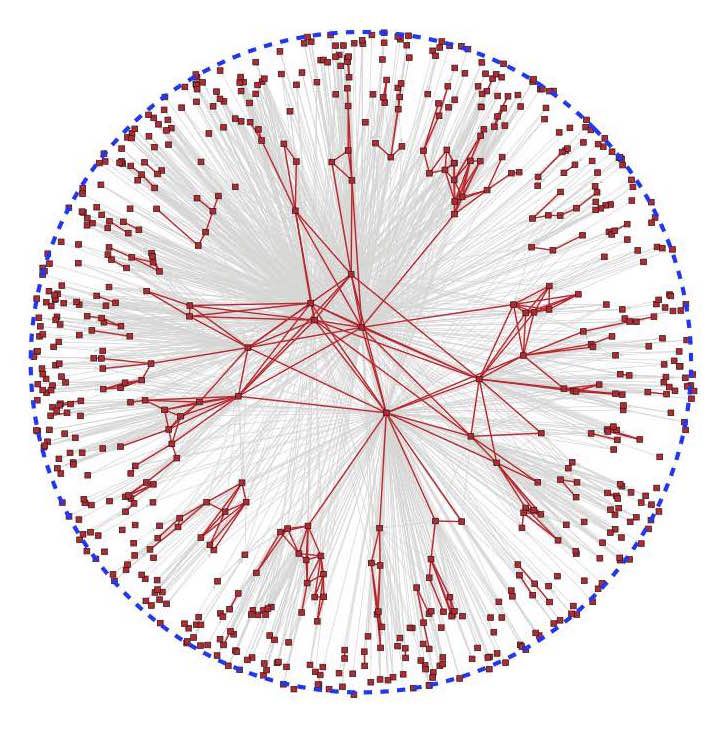
All real networks are different, but many have some structural properties in common. There seems to be no consensus on what the most common properties are, but scale-free degree distributions, strong clustering, and community structure are frequently mentioned without question. Surprisingly, there exists no simple generative mechanism explaining all the three properties at once in growing networks. Here we show how latent network geometry coupled with preferential attachment of nodes to this geometry fills this gap. We call this mechanism geometric preferential attachment (GPA), and validate it against the Internet. GPA gives rise to soft communities that provide a different perspective on the community structure in networks. The connections between GPA and cosmological models, including inflation, are also discussed.
Cosmological networks
Marián Boguña, Maksim Kitsak, Dmitri Krioukov,
NEW JOURNAL OF PHYSICS
(2014)
abstract
Networks often represent systems that do not have a long history of study in traditional fields of physics albeit, there are some notable exceptions, such as energy landscapes and quantum gravity. Here, we consider networks that naturally arise in cosmology. Nodes in these networks are stationary observers uniformly distributed in an expanding open Friedmann-Lemaitre-Robertson-Walker universe with any scale factor and two observers are connected if one can causally influence the other. We show that these networks are growing Lorentz-invariant graphs with power-law distributions of node degrees. These networks encode maximum information about the observable universe available to a given observer.
Network Cosmology
Krioukov, Maksim Kitsak, Sinkovits, Robert S. Rideout, David Meyer, David Marian Boguña,
SCIENTIFIC REPORTS
(2012)
abstract
Prediction and control of the dynamics of complex networks is a central problem in network science. Structural and dynamical similarities of different real networks suggest that some universal laws might accurately describe the dynamics of these networks, albeit the nature and common origin of such laws remain elusive. Here we show that the causal network representing the large-scale structure of spacetime in our accelerating universe is a power-law graph with strong clustering, similar to many complex networks such as the Internet, social, or biological networks. We prove that this structural similarity is a consequence of the asymptotic equivalence between the large-scale growth dynamics of complex networks and causal networks. This equivalence suggests that unexpectedly similar laws govern the dynamics of complex networks and spacetime in the universe, with implications to network science and cosmology.